cuda-tutorial
7.1 逐次での疑似乱数生成
並列での乱数生成の前に逐次で標準的な疑似乱数を紹介する。
7.1.1 線形合同法
C言語のrand()は線形合同法を採用している。 初期値xについて
int rand(int *x){
int A = (大きな素数);
int B = (大きな素数 != A);
*x = A * *x + B;
return *x;
}
という手続きで乱数を生成する。 xはオーバーフローを起こすと下32bitを残して切り捨てる。 極めて簡単な実装でそれらしい振る舞いをしてくれるが、多くの問題点がある。
まず、周期が短いことだ。int32型での周期は最大2^32で、シミュレーションで容易に1周できる。 その上、小さい桁の乱数性が低く、必ず偶数と奇数を交互に繰り返してしまう。 (バンダイナムコ発売のガルドセプト サーガにてダイスの目が偶数か奇数か予測出来るバグ[1]の原因がおそらくこれ) さらに多次元にて秩序が見られる[2]。
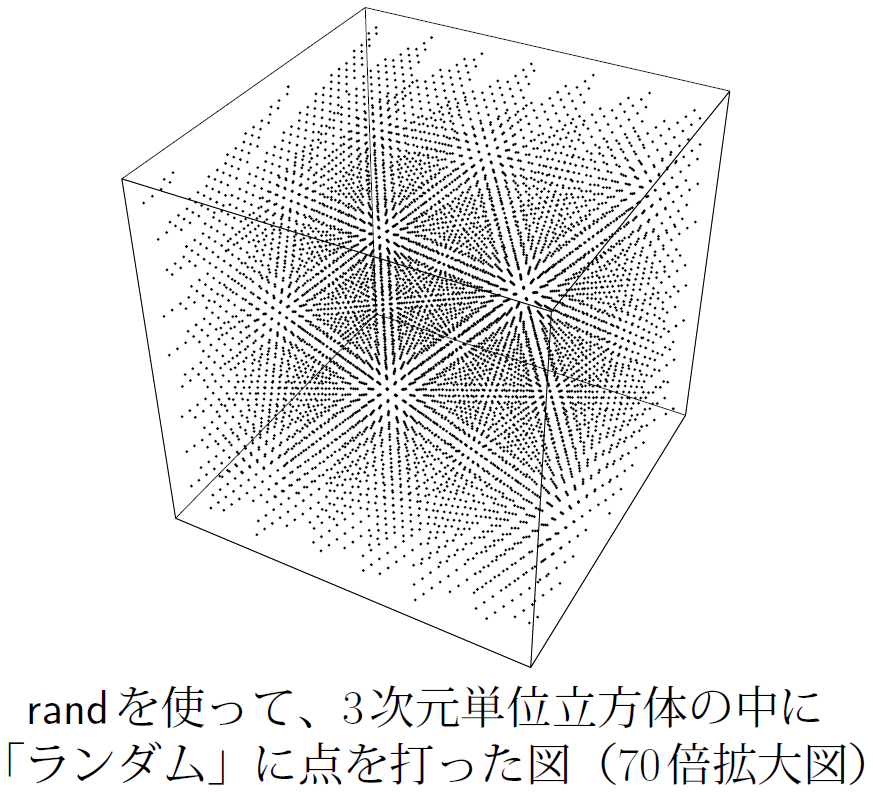
間違いだらけの疑似乱数選び[2]より引用
7.1.2 Mersenne-Twister
線形合同法での様々な問題点を解決するのがMersenne-Twister[3]である。
アルゴリズムの詳細は省くが、これを用いて適切なパラメーターを指定することで、計算速度は線形合同法と大差ないにも関わらず、周期が2^19937-1となり、高次元均等分布を実現する(623次元超立方体中に均等に分布することが示されている)。
これがいわゆるMT19937で、一般的にMersenne-Twisterによる疑似乱数と呼ぶ時、MT19937を指す。
MT19937のアルゴリズムはホームページからダウンロードが出来る他、C++11以降の標準ライブラリ<random>に採用されている。
Links
引用、紹介
[1] Culdcept Saga (Fake Dice) [2] 間違いだらけの疑似乱数選び [3] Mersenne Twister Home Page